Циклический алгоритм примеры
- АлгоритмыЦиклический алгоритм примеры
Аннотация: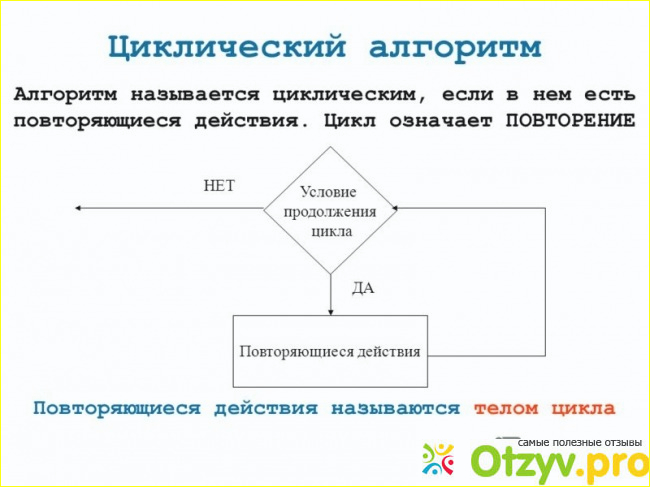
Набор фильтров кода разнесения передачи (TDCFS), принятый в ATSC3.0, представляет собой метод с использованием линейных фильтров с полным проходом для минимизации возможности взаимной помехи среди передаваемых сигналов. В настоящем документе представлен новый циклический алгоритм для проектирования набора фильтров в TDCFS. В случае проектирования фильтра, имеющего почти идентичное свойство корреляции, предлагаемый алгоритм требует меньше времени итерации, чем алгоритм из литературы, из-за его простоты в вычислении.
Таким образом, его можно использовать для разработки набора фильтров, состоящего из огромного количества фильтров и фильтров с длинными последовательностями с относительно меньшей сложностью по сравнению с алгоритмами в литературе. В этом документе также приводится численный пример и результаты моделирования системы, чтобы продемонстрировать лучшую производительность, чем в уровне техники.
Обнаружить цикл на графике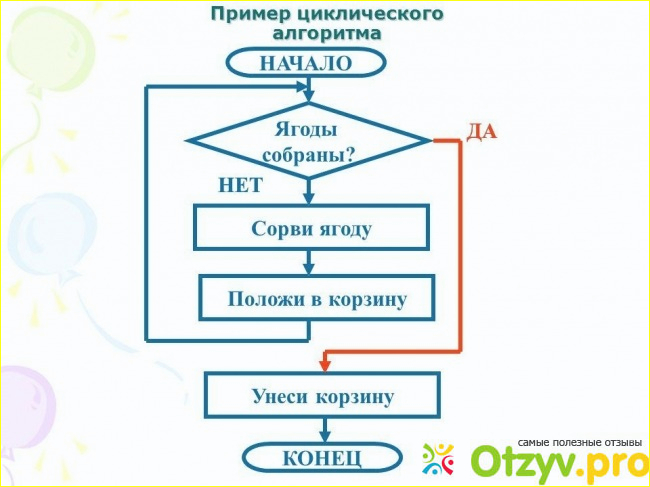
1. Учитывая ориентированный граф, проверьте, содержит ли граф цикл или нет. Ваша функция должна возвращать значение true, если данный график содержит хотя бы один цикл, иначе возвращает false. Например, следующий график содержит три цикла 0-> 2-> 0, 0-> 1-> 2-> 0 и 3-> 3, поэтому ваша функция должна возвращать true.
2. Рекомендуется: сначала разрешите его на « ПРАКТИКЕ », прежде чем перейти к решению.
3. Depth First Traversal может использоваться для определения цикла на графике. DFS для связанного графика создает дерево. На графике есть цикл, только если на графике есть задний край. Задний край - это ребро, которое от узла к себе или один из его предков в дереве, создаваемом DFS. На следующем графике имеется 3 задних края, отмеченных знаком перекрестка. Мы можем заметить, что эти 3 задних края показывают 3 цикла, присутствующие на графике.
4. Для несвязанного графика мы получаем лес DFS как результат. Чтобы обнаружить цикл, мы можем проверить цикл на отдельных деревьях, проверив обратные края.
5. Чтобы обнаружить задний край, мы можем отслеживать вершины, находящиеся в настоящее время в стеке рекурсии функции для обхода DFS. Если мы достигнем вершины, которая уже находится в стеке рекурсии, тогда в дереве есть цикл. Кромка, соединяющая текущую вершину с вершиной в стеке рекурсии, представляет собой задний край. Мы использовали массив recStack [] для отслеживания вершин в стеке рекурсии.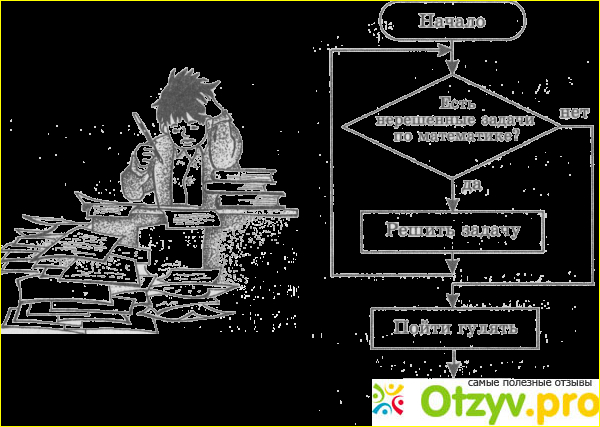
Проверка циклического избыточности и модуль Modulo-2
CRC или Cyclic Redundancy Check - это метод обнаружения случайных изменений / ошибок в канале связи.
CRC использует Generator Polynomial, который доступен как на стороне отправителя, так и на стороне получателя. Пример генераторного полинома имеет вид, подобный x 3 + x + 1. Этот генераторный многочлен представляет собой ключ 1011. Другим примером является x 2 + 1, представляющий ключ 101.
Сторона отправителя (Генерация закодированных данных из данных и полинома генератора (или ключа)):
1. Двоичные данные сначала дополняются добавлением нулей k-1 в конце данных
2. Используйте двоичное деление по модулю 2, чтобы разделить двоичные данные на ключ и сохранить остаток деления.
3. Добавить остаток в конце данных для формирования закодированных данных и отправить их,
Сторона приемника (проверьте, есть ли ошибки, введенные в передаче).
Выполните модульное деление еще раз, а если остаток равен 0, то ошибок нет.
В этой статье мы сосредоточимся только на поиске остатка, т. е. контрольном слове и кодовом слове.
Модуль 2: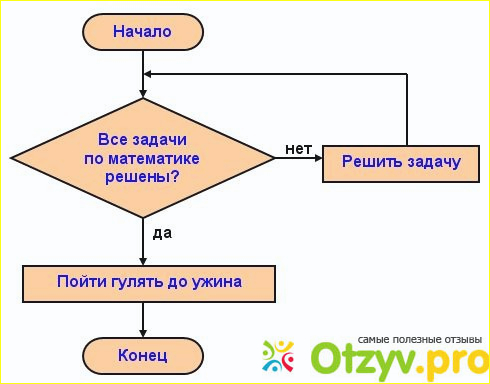
Процесс модульного двоичного деления по модулю-2 такой же, как и обычный процесс разделения, который мы используем для десятичных чисел. Именно поэтому вместо вычитания мы используем XOR здесь.
§ На каждом шаге копия делителя (или данных) имеет XORed с k битами дивиденда (или ключа).
§ Результатом операции XOR (остаток) является (n-1) бит, который используется для следующего шага после выталкивания 1 дополнительного бита, чтобы сделать его n бит длинным.
§ Когда нет бит, оставшихся вниз, у нас есть результат. (N-1) битный остаток, который добавляется на стороне отправителя.
Пример 1
Обратите внимание, что CRC в основном разработан и используется для защиты от распространенных ошибок на каналах связи и НЕ подходящей защиты от преднамеренного изменения данных.
Циклическое сокращение
Циклическая редукция - это численный метод решения больших линейных систем путем многократного расщепления задачи. Каждый шаг исключает четные или нечетные строки и столбцы матрицы и остается в аналогичной форме. Шаг исключения относительно дорог, но расщепление проблемы позволяет проводить параллельные вычисления.
Применимость
Метод применим только к матрицам, которые могут быть представлены в виде (блочной) матрицы Теплица, такие проблемы часто возникают в неявных решениях уравнений в частных производных на решетке. Например, быстрые решат для уравнения Пуассона выражают проблему как решение трех диагональной матрицы, дискредитируя решение на регулярной сетке.
Точность
Системы, которые имеют хорошую численную стабильность, изначально стремятся к лучшему с каждым шагом до точки, где может быть дано хорошее приближенное решение [1], но поскольку специальная матричная форма должна быть сохранена, поворот не может быть выполнен для улучшения числовой точности.
Сравнение с multigrid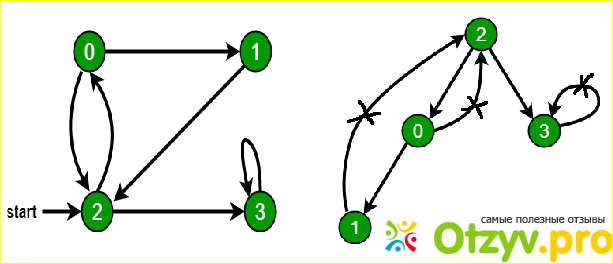
Этот метод не является итеративным, он ищет точное решение линейной задачи, согласующейся с заданными граничными значениями, контрастирует с аналогичным, но вычислительно более дешевым многосеточного метода, который распространяется на оценки погрешности коррекции и учитывает различные параметры релаксации в разных масштабах, итеративный аспект, позволяющий лучше включать нелинейные функции.
Комбинация с быстрым преобразованием FFT
Преобразование из пространственной области и повторение PDE называется спектральным методом, анализ Фурье и циклическое восстановление объединяются в алгоритм FACR [2], который поясняется в «Численных рецептах» - см. 19.4. Методы циклического восстановления для краевых задач.
Обнаружение цикла и алгоритм стека
Предположим, что нам задана функция f, которая отображает некоторую область D в себя.
Учитывая начальный элемент x 0 из D, определим бесконечную последовательность x 1 = f (x 0), x 2 = f (x 1) и т. Д.
Если область D конечна, то в конечном итоге некоторый элемент в последовательности должен повториться,
и с этого момента последовательность будет повторяться снова и снова.
Последовательность будет «падать» в цикл.
Проблема обнаружения цикла требует обнаружения того, что последовательность стала периодической,
и найти длину цикла.
Обнаружение цикла возникает в ряде ситуаций:
Кнут обсуждает его в контексте анализа генераторов случайных чисел.
В 3-м издании «Искусство компьютерного программирования», том. 2, упражнения 3.1-6,7,
он представляет и сравнивает несколько известных алгоритмов.
Мы могли бы захотеть обнаружить, когда, скажем, конфигурация сотового автомата стала периодической,
и найдите ее период.
Известные методы Роллана для факторизации и дискретных логарифмов основаны на обнаружении циклов.
(Алгоритм, представленный здесь, однако, не может быть применен к методу факторизации по.)
Я обнаружил алгоритм, представленный здесь в октябре / ноябре 2002 года. Алгоритм требует,
чтобы на D было определено полное упорядочение. Для простоты предположим, что D - конечное
множество целых чисел.
Базовый алгоритм стека
Наш базовый алгоритм выглядит следующим образом: Храните стек пар (на i, i), где, во всяком случае,
и i, и на i в стеке образуют строго возрастающие последовательности. Стек изначально пуст.
На каждом шаге j поп из стека все записи (на i, i), где на i > на j. Если на i = на j найдено в стеке,
мы закончили;, то длина цикла равна j - i. В противном случае нажмите (x j, j) поверх стека и продолжить.
Этот алгоритм всегда останавливается на наименьшем значении цикла последовательности x min при
втором вхождении этого значения: как только x min добавляется в стек при первом появлении, он никогда не удаляется. Следовательно, алгоритм остановится, когда он встретит x min во второй раз. С другой стороны,
любое другое значение цикла больше x min, поэтому оно будет удалено с помощью x min,
прежде чем появится возможность снова появиться.
Пусть n - время остановки алгоритма. Можно показать, что размер стека с большой вероятностью
ограничен O (log n) (т. Е. Вероятность стремится к 1 при стремлении n к бесконечности).
Поэтому алгоритм требует только логарифмического объема памяти.
Вышеизложенное предполагает, что величины значений последовательности.
Если эти величины заранее известны, чтобы иметь закономерности, мы вместо этого сравниваем их соответствующие хеши.
Техника секционирования
Базовый алгоритм стека останавливается в равномерно случайной точке во втором цикле
через цикл последовательности.
Чтобы увеличить вероятность остановки ближе к началу второго цикла, добавив практически
никакого дополнительного штрафа за каждый шаг, мы вводим следующий метод разбиения.
Для некоторого целого k разделим область D на k непересекающихся классов. Мы могли бы, например,
рассмотреть остаток по модулю каждого значения x i. Мы сохраняем отдельный стек для каждого класса. На каждом шаге i мы сначала определяем, к какому классу x i, принадлежит, а затем вставляем (x i, i) в соответствующий стек. Мы называем это с несколькими стеками.
Почему все еще работает? Потому что, когда появляется значение x i, оно всегда отправляется
в один и тот же стек. Кроме того, поскольку на каждом этапе работает на одном стеке, время
выполнения на шаге остается практически неизменным. Более того, алгоритм останавливается всякий раз,
когда в первую очередь стеки обнаруживают повторение.
Каждый класс j, 0<= j < k, содержит свой собственный минимальный цикл x min, j.
Каждый x min, j распределяется равномерно и независимо случайным образом в цикле.
Отсюда следует, что расстояние от начала цикла до первого минимума составляет в среднем
долю 1 / (k +1) длины цикла.
Любой алгоритм должен, очевидно, работать, по крайней мере, до начала второго цикла.
Итак, если взять, например, k = 100, то наше время работы будет всего на 1% от длины цикла выше
абсолютного минимума.
Что происходит с требованиями к памяти? При использовании k стеков размер каждого уменьшается
на O (log k), небольшое количество. Поэтому, поскольку у нас есть k стеков,
общая используемая память грубо умножается на k.
Видео обзор
| Все(5) |
|---|
 Урок и 31 32 Циклические алгоритмы 5мин 16с Урок и 31 32 Циклические алгоритмы 5мин 16с |  Циклические алгоритмы Циклические алгоритмы |  Циклические алгоритмы Циклические алгоритмы |  ОГЭ по информатике. Задание 9. Циклические алгоритмы. Разбор типичных примеров. ОГЭ по информатике. Задание 9. Циклические алгоритмы. Разбор типичных примеров. |  6 Циклический алгоритм в блок-схемах: примеры с предусловием, с постусловием 6 Циклический алгоритм в блок-схемах: примеры с предусловием, с постусловием |




Комментарии на отзыв: