
Частное это что в математике
- Математика любит точность. Учим частное числоМатематические действия.
Частное.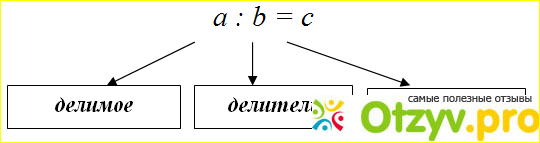
Введение.
Пройдемся по азам математики и узнаем, что такое частное и как его получить.
Определение.
Частное чисел - это результат, полученный делением одного числа, назовем его а), на другое число, названное б). При этом, сделаем разбор чисел.
На рисунке (1) показан пример деления одного числа (а) на другое число (б), в результате получается число с), где:
а) - делимое;
б) - делитель;
с) - частное.
Чтобы получить частное двух чисел, необходимо делимое поделить на делитель.
Можно совершать и обратные действия, скажем, получая путем умножения частного на делитель можно получить делимое.
Пример 1.
Приведем самый простой пример получения частного числа, на примере таблицы умножения.
Из примера: 2*4=8, получаем:
8:4=2, где
8- делимое;
4- делитель;
2- частное.
Пример 2.
Возьмем пример по сложнее, например, найти частное чисел 48:12, получаем
48:12=4
Частное чисел 48 и 12 равно 4.
Пример 3.
Найти частное чисел 120 и 15.
Чтобы решить данную задачу, составим пример и получаем:
120:15=8, где:
120 - делимое,
15 - делитель,
8 - частное.
Ответ - 8.
Пример 4.
Найти частное чисел 975 и 13.
Решаем задачку таким образом, как и предыдущие и получится:
975:13=75.
Ответ - 75.
Пример 5.
Найти частное двух чисел 102,06 и 12,6.
Решаем задачу таким образом, что составляем пример с делением одного числа на другое и получаем:
102,06:12,6=8,1.
Наш ответ - 8,1.
Если просят найти частное чисел больших, а так же десятичных дробей, тогда следует воспользоваться способом деления в столбик. При этом, может получиться не целое число, а число с остатком.
Такие примеры с делением начинаются в начальных классах, поэтому важно для себя не просто запомнить, как называется то или иное число в конкретном математическом примере, но и понять взаимосвязь. Так, как вы уже догадались, прослеживается связь делимого, делителя и частного и из одного вытекает другое.
Взаимосвязь.
Другими словами, чтобы получить частное, нужно делимое поделить на делитель. Чтобы получить делимое, нужно частное умножить на делитель. Чтобы получить делитель, необходимо делимое умножить на частное.
Из простых примеров становится понятно, что частное - самое маленькое из всех трех чисел в действии с делением.
Рисунок 2.

Наверху с числами множитель, множитель и произведение выполнено действие умножения. То есть первый множитель равен 3, второй множитель равен 2, в результате умножения между собой двух множителей получается произведение. Из этого примера очень просто совершить обратное действие между тремя числами, поменяв их местами, то есть сделав все в обратном порядке, но только заменив умножение на деление. Таким образом, 3*2=6, а
6:2=3, где
6 - делимое (которое в первом примере было произведением), самое большое число,
2 - делитель, которое в первом примере служило множителем, и было самым маленьким числом,
3 - частное, которое в примере с произведением было множителем.
Совершать математические действия умножения и деления просто, как и в примерах с вычитанием и сложением, только нужно во первых знать таблицу умножения, либо пользоваться способом деления чисел в столбик, особенно в случае с большими числами и числами с остатком.
Зная взаимосвязь чисел можно составлять самостоятельно примеры и действовать в любом порядке и в прямом или обратном направлении.
Произведение-это умножение
а частное-это деление!

Вот такие слова про математику, очень точную науку должен знать каждый и уважать правила математики. Ведь все в этой точной науке объясняется правилами. С помощью правил вы можете решить даже самые сложные задачи. Конечно, помимо правил, вы должны понимать, о чем речь и включать свою логику в решении сложных задач. Даже если на первый взгляд кажется, что задача перед вами стоит невыполнимая, подумайте и представьте мысленно в голове, о чем речь. Переведите непонятные на первый взгляд примеры в простые ассоциации и тогда вам станет гораздо легче ориентироваться.
Математика - точная наука.
Вопрос, может ли частное число быть меньше, чем делимое или делитель? Ответ: да, может.
Частное число может быть и меньше делителя. Частное двух чисел будет самым маленьким, если делимое меньше, чем делитель. То есть не обязательно делимое - самое большое число. Можно составить такую задачку, в которой делимое будет меньше делителя, например:
Найти частное чисел 8 и 16, где 8 - делимое, а
16 - делитель.
Тогда составляем пример:
8:16=0,5.
Вот и получается, что 0,5 - частное, которое и является самым маленьким числом и даже меньше, чем делитель, а делитель - не всегда самое маленькое число. Как вы видите из примера, 16 - делитель и его значение самое большое.
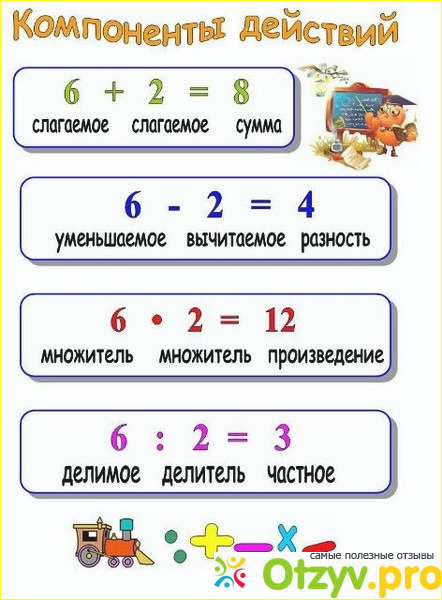
Давайте, раз уж мы заговорили обо всех примерах точной науки, напомним все названия компонентов действия.
Первое. При сложении. В примере со сложением у нас есть первое слагаемое, второе слагаемое и сумма, полученная в результате сложения двух слагаемых. Обратное действие:
Второе. При вычитании. Уменьшаемое, вычитаемое и разность, где уменьшаемое - число, из которого вычитают, вычитаемое - второе число, которое вычитают и разность двух чисел уменьшаемого и вычитаемого. Разность.
Третье. Умножение. Первый множитель умножают на второй множитель и получают произведение.
Четвертое. При делении. Делимое "поделить" на делитель, получится частное.
А:Б=В.
В - частное.
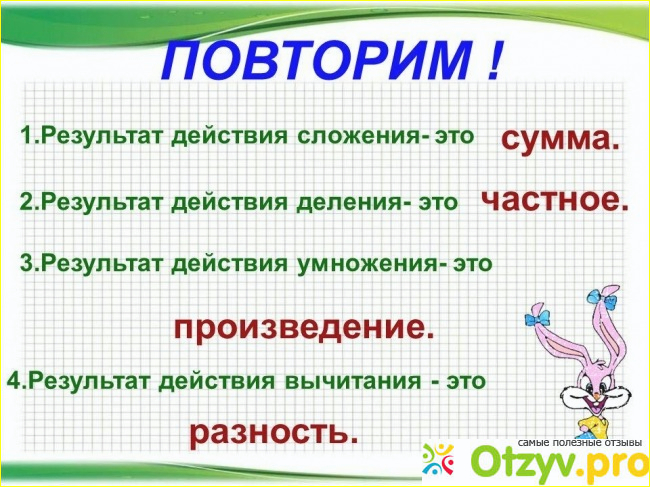
А теперь повторите еще раз все действия в математике.
Объясните своими словами, какие действия нужно совершить, чтобы получить сумму? А чтобы получить Частное? Далее, произведение? И наконец, разность?
Вы теперь поняли, какое число называется Частным? А вы сможете своими словами объяснить, какие действия следует совершить, чтобы получилось частное двух чисел? Если да, то тогда составьте свой пример. Пускай он будет самым простым и будет взят из таблицы умножения, либо вы хотите потренироваться на более сложных числах? Тогда возьмите число в виде дроби или с остатком и произведите расчет частного двух чисел путем деления столбиком.
Математика любит точность. Поэтому понимайте правила, но, если на первый взгляд кажется сложным и нереальным решить задачку с умножением или делением, пользуйтесь подсказками и когда весь процесс решения задачи пойдет у вас на автомате, вам решать задачки понравится. Ведь всегда приятно найти разгадку, получить решение или ответ!
Заключение.
Зная азы математики, можно научиться очень ловко обращаться с числами, цифрами и вычислениями, тем более это умение вам пригодится в будущем. Точность никогда не будет лишней! А умение складывать, вычитать, умножать или делить в уме, сэкономит ваше время и сделает вас более эрудированным и грамотным человеком. Возможно ваша будущая профессия будет связана с математикой, именно поэтому со школьной скамьи вы должны научиться быстро и правильно считать в уме! А такие простые действия, как получение произведения или частного вам обязательно пригодятся!
Важно не просто зазубрить, но и понять смысл, и хотя математика называет себя точной наукой, при ее понимании можно тоже включать логику.
Поняли? Хотите больше информации по данной теме по частные числа? Тогда смотрите видеоматериал Математика 4 класса. 26 октября. Остаток от деления.
Видео обзор
| Все(5) |
|---|
 Математика 4 класс. 26 октября. Частное и остаток от деления Математика 4 класс. 26 октября. Частное и остаток от деления |  Основные понятия дифференциальных уравнений от bezbotvy Основные понятия дифференциальных уравнений от bezbotvy |  Деление методом неполного частного Деление методом неполного частного |  Отношение, Математика, 6 класс (Частное двух чисел.) Отношение, Математика, 6 класс (Частное двух чисел.) |  6 класс. Отношения. 6 класс. Отношения. |








Комментарии на отзыв:
Я бы хотела привести несколько примеров, которые помогут лучше понять, как работает это понятие в математике. Например, если мы возьмем числа 24 и 6, то частное будет равно 4. Это означает, что 24 можно разделить на 6, получив 4. Также можно рассмотреть пример с числами 100 и 25, где частное будет равно 4. Это означает, что 100 можно разделить на 25, получив 4.
Я считаю, что понимание понятия частного в математике очень важно для того, чтобы успешно решать задачи и примеры в школе и в жизни. Это понятие помогает нам лучше понимать взаимосвязь между делимым, делителем и частным. Кроме того, оно может быть полезно в решении финансовых задач, например, при расчете скидок или налогов.
В целом, я очень довольна тем, что изучаю математику и понимание понятия частного - одно из тех знаний, которые будут мне полезны в жизни. Я советую всем, кто интересуется математикой, углубиться в изучение этого понятия и узнать, как оно может быть применено в различных сферах жизни.