
Прямоугольная трапеция
- Прямоугольная трапеция 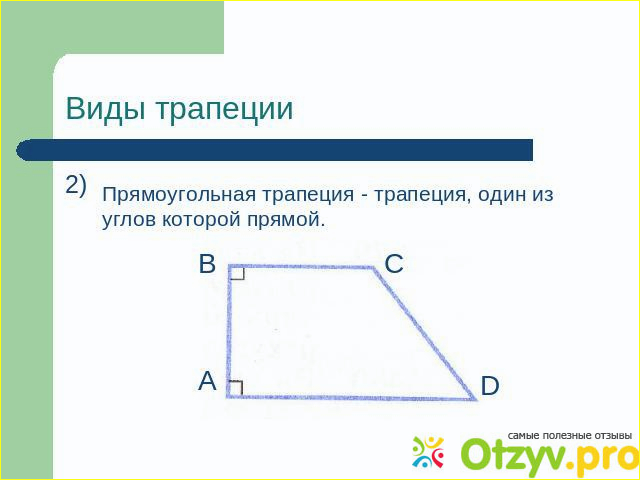 Один из вариантов удобных для решения задач трапеции - это прямоугольная трапеция, определение вы видите на слайде, причём из свойства того,
Один из вариантов удобных для решения задач трапеции - это прямоугольная трапеция, определение вы видите на слайде, причём из свойства того,
что один угол является прямым, то вследствие свойств параллельных прямых, коими и являются основания этой самой фигуры, которых пересекает третья, то бишь боковая сторона, следует, что односторонний угол также будет прямым, следовательно в прямоугольной трапеции два прямых угла.
По мне так это прямоугольник, у которого покосилась одна из сторон, а остальные остались на месте.
Чем удобна прямоугольная трапеция так это тем, что боковая сторона, которая перпендикулярна обоим основаниям ещё является по совместительству очень удобным отрезком и важным для задач - высотой этой самой трапеции.
Таким образом площадь трапеции можно вычислить по трём сторонам трапеции: это должны быть основания и та сама боковой сторона, которая составляет с ними прямые углы: для нашего рисунка со слайда формула будет следующей S=(AD+BC)*AB/2
А если из другой вершины, которая принадлежит меньшему основанию, то есть в нашем случае из точки B, провести высоту, то трапецию разделиться на две фигуры: прямоугольник и прямоугольный треугольник, очень удобно при решении задач с данным видом трапеции.
Опять же если боковые стороны трапеции продлить до точки из пересечения, то продленные боковые стороны вместе с бОльшим основаниям составят опять же прямоугольный треугольник.
Видео обзор
| Все(5) |
|---|
 Задача 6 №27633 ЕГЭ по математике. Урок 74 Задача 6 №27633 ЕГЭ по математике. Урок 74 |  ОГЭ по математике. Задание 11. Прямоугольная трапеция. Тангенс ОГЭ по математике. Задание 11. Прямоугольная трапеция. Тангенс |  Геометрия 8. Урок 6 - Трапеция Геометрия 8. Урок 6 - Трапеция |  Это очень просто -- ЛЕНТОЧНАЯ РЕЗЬБА. Это очень просто -- ЛЕНТОЧНАЯ РЕЗЬБА. |  Задание 15 Прямоугольная трапеция Задание 15 Прямоугольная трапеция |



Комментарии на отзыв: