Объем трапеции

В геометрии, трапецеидальный призмы представляет собой твердую форму, которая имеет трапецию (или трапецию в Великобритании) сечения в одном направлении и прямоугольного сечений в других направлениях. Для того, чтобы вычислить объем симметричной трапециевидной призмы, вы должны знать, четыре измерения: длина призмы L, высоту трапецеидального поперечного сечения H, ширина основания трапеции B, а также верхнюю ширину трапеции A ,

С другой стороны, если вы знаете трапеции боковые наклонная длин S, можно вычислить объем с L, S, B и A.

Обе формулы для объема трапециевидной пирамиды приведены ниже вместе с несколькими проблемами например. Смотрите также, Поверхность Формула зоны для трапециевидной Prism.

Формула для тома трапециевидной Prism

Если длина призмы L, трапецию ширина основания B, трапецию ширина верхней поверхности А, а высота трапецию Н, то объем призмы задается четырьмя переменной формулой:

V (L, В, А, Н) = ЛГ (А + В) / 2.

• Другими словами, перемножить длину, высоту и среднее число А и В.

  Эта формула эквивалентна умножения длины призмы по площади трапециевидных сечений. Если вы не знаете, H, но вместо того, чтобы знать боковую наклонная длина S, формула немного сложнее. Это:

V (L, В, А, С) = Л (А + В) SQRT (4S2 + 2AB - В2 - А2) / 4.

Эта вторая формула получена из того факта, что:

H = SQRT [S2 - ((B - A) / 2) 2]

= SQRT (4S2 + 2AB - B2 - A2) / 2.

Вот несколько примеров проблем, которые помогут вам выработать призм объемы. В приведенных выше формулах и примерах, приведенных ниже, предполагается, что трапеций являются симметричными, то есть боковые наклонная длины равны с обеих сторон и в центре верхней длины выровнены по вертикали с центром базовой длины.

Пример 1

Трапецеидальной призмы имеет длину 8, ширину основания 7, ширина верхней части 4, и высоту 3.

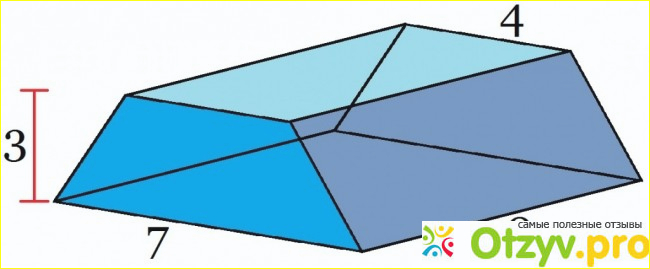
Используя Н = 3, В = 7, А = 4 и L = 8, можно вычислить объем, используя первое уравнение. Затыкать переменные в этом уравнении дает нам:

V = ЛГ (А + В) / 2

= 8 * 3 * (4 + 7) / 2

= 24 * 11/2

= 132.

Пример 2

Трапециевидную пирамида имеет длину 6,03 см. Его ширина основания составляет 7,82 мм, ширина верхней 3,55 см, а наклонная сторона длина 4,71 см. Каков его объем в кубических сантиметрах?

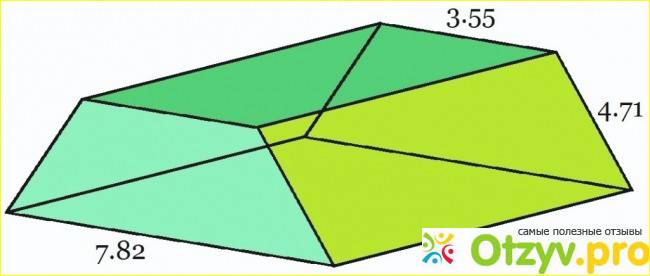
Эта проблема дает L = 6,03, В = 7,82, А = 3,55 и S = 4,71. Так как мы имеем S вместо H, мы используем второе уравнение объема. Подключение этих значений дает нам:

V = L (А + В) SQRT (4S ^ 2 + 2AB - B ^ 2 - Л ^ 2) / 4

= 6,03 (3,55 + 7,82) SQRT (4 * 4,71 ^ 2 + 2 * 3,55 * 7,82 - 7,82 ^ 2 - 3,55 ^ 2) / 4

= 143.92 см ^ 3.

Таким образом, объем 143.92 кубических сантиметров или, что эквивалентно 0,14392 литра.

Пример 3

Трапециевидной призмы имеет объем 1950 кубических дюймов. Высота составляет 6 дюймов, длина 25 дюймов, а верхняя ширина составляет 11 дюймов. Какова ширина трапеции основания?

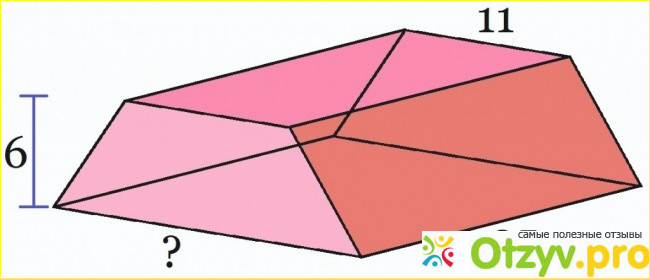
Здесь нам дают объем, но один из измерений отсутствует. Мы имеем V = 1950, Н = 6, L = 25, а = 11, но B неизвестна. Поэтому нам нужно подключить эти значения в первую формулу объема и решить для B. Это дает нам:

V = ЛГ (А + В) / 2

1950 = 25 * 6 * (11 + В) / 2

1950 / (25 * 6) = (11 + В) / 2

13 = (11 + В) / 2

2 * 13 = 11 + B

26 = 11 + B

26 - 11 = В

15 = B

Таким образом, ширина основания составляет 15 дюймов.

Исчисление Оптимизация Пример: Увеличить объем трапеции Prism с заданной длины и базы

Предположим, вы хотите, чтобы сделать коробку в форме трапециевидной призмы субъекта к этим трем условиям: длина коробки призмы должна быть 24 см, одна из параллельных сторон трапеции лица должны быть длиной 12 см, а по всему периметру трапециевидной лицо должно быть 34 см. Какую форму трапеции должно быть таким, чтобы объем коробки максимизируется?

Прежде всего, следует отметить, что это, по сути задача о максимизации площади трапециевидных сечений, так как длина постоянна и равна 24 см.

Для того, чтобы придумать уравнения, мы должны оптимизировать с исчислении, сначала пусть х равняться длине каждой стороны наклонной. Так как одна из параллельных сторон 12, другой должен быть 34 - 12 - х - х или 22 - 2x. Ниже приведены возможные формы трапеции, которые соответствуют ограничениям задачи; треугольник и плоская линия являются предельными случаями.

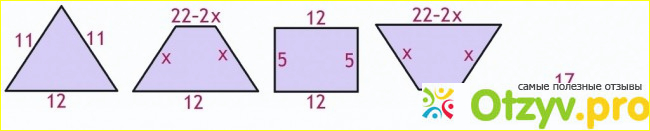
Видео обзор

Нахождение объема тела вращения с помощью интеграла

ЕГЭ В6. Площадь прямоугольной трапеции. Видео урок.

Нахождение объема тела вращения методом слоев

3 Основы Роста Мышц | Программа "Путь Геракла"

Интеграл для вычисления объема тела, полученного при вращении плоской фигуры.